Nesse post quero apresentar uma versão intuitiva e informal deste clássico experimento idealizado por Fisher. Versões mais formais e alinhadas aos conceitos utilizados atualmente com testes de hipóteses podem ser encontradas facilmente na internet.
Introdução
O experimento “Lady Tasting Tea” tornou-se um marco na história da estatística por mostrar, de forma clara e acessível, como um teste de hipótese pode ser estruturado.
A essência está em três passos:
- Definir a hipótese nula — a suposição inicial de que não existe efeito ou habilidade especial;
- Planejar um desenho experimental controlado — de modo que o acaso seja a única explicação plausível sob a hipótese nula;
- Estabelecer um critério de decisão — que permita avaliar se o resultado observado é suficientemente raro para rejeitar o acaso.
No caso apresentado por Fisher, a alegação era simples: distinguir, ao provar uma xícara de chá com leite, se o leite foi colocado antes ou depois. O mérito do exemplo está em como essa afirmação foi transformada em um teste sistemático e replicável, conectando o raciocínio estatístico a um procedimento experimental claro e objetivo.
Experimento
Em 1935, o estatístico Ronald A. Fisher publicou o livro The Design of Experiments.

Um dos exemplos mais famosos que ele apresentou foi o da “Lady Tasting Tea” (A dama provando o chá), usado para ilustrar como projetar um experimento e testar hipóteses de forma sistemática.
Imagine a seguinte situação:
Durante um chá, uma colega de Fisher, a Dra. Blanche Muriel Bristol, afirmou que conseguia distinguir se o leite tinha sido colocado antes ou depois do chá na xícara.
Fisher propôs um procedimento para verificar a alegação:
- Seriam preparadas 8 xícaras, fora da vista da Dra. Bristol: 4 com leite antes e 4 com chá antes.
- A ordem de apresentação das xícaras seria aleatorizada, garantindo que apenas o paladar pudesse influenciar o resultado.
- A Dra. Bristol saberia que havia 4 de cada tipo, mas não sabia quais eram.
- Sua tarefa: identificar todas as xícaras com leite antes.
Ela acertou as 4 xícaras. E agora? Foi sorte ou habilidade?
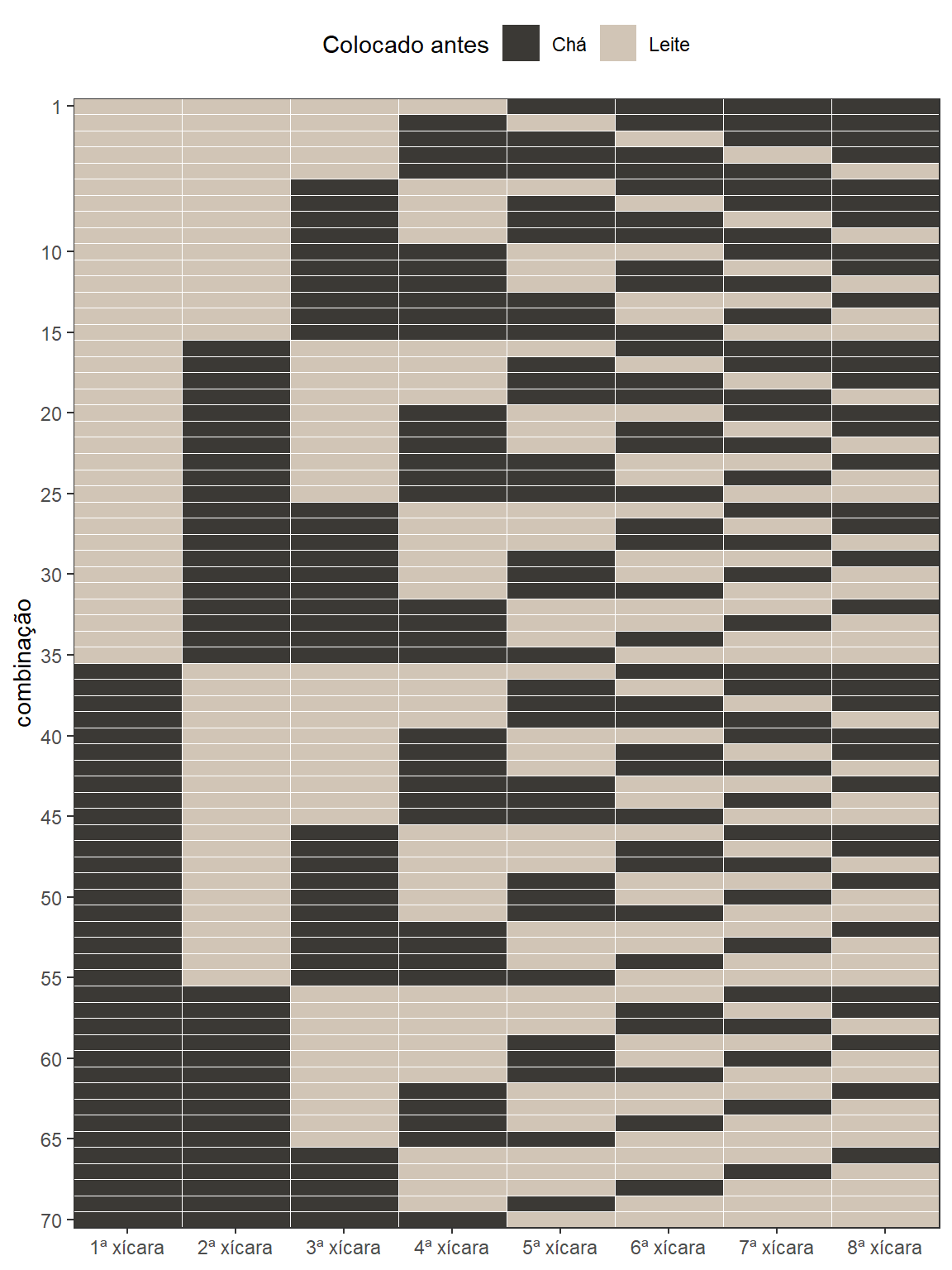
A hipótese nula de Fisher era que ela não possuía nenhuma habilidade especial. Se isso for verdade, qualquer acerto seria puro acaso. A seguir, visualizamos todas as maneiras possíveis de dispor 8 xícaras, sendo 4 com chá antes e 4 com leite antes.
Existem exatamente 70 combinações possíveis. Como a ordem das xícaras foi aleatorizada, sob a hipótese nula, cada uma dessas 70 combinações é igualmente provável. Apenas uma delas corresponde ao acerto de todas as 4 xícaras com leite antes.
Vamos supor que a combinação correta sorteada é dada pela seguinte combinação:
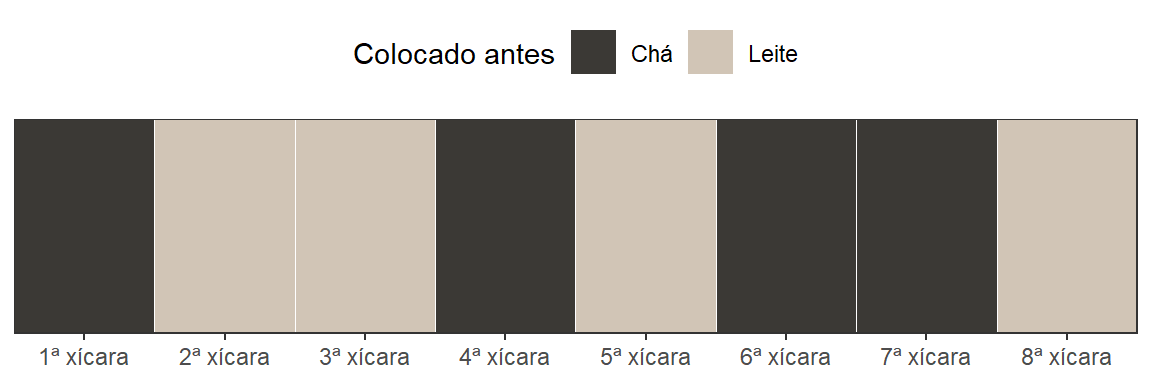
Vamos organizar as 70 combinações de acordo com o número de acertos das xícaras em que se colocou leite antes:
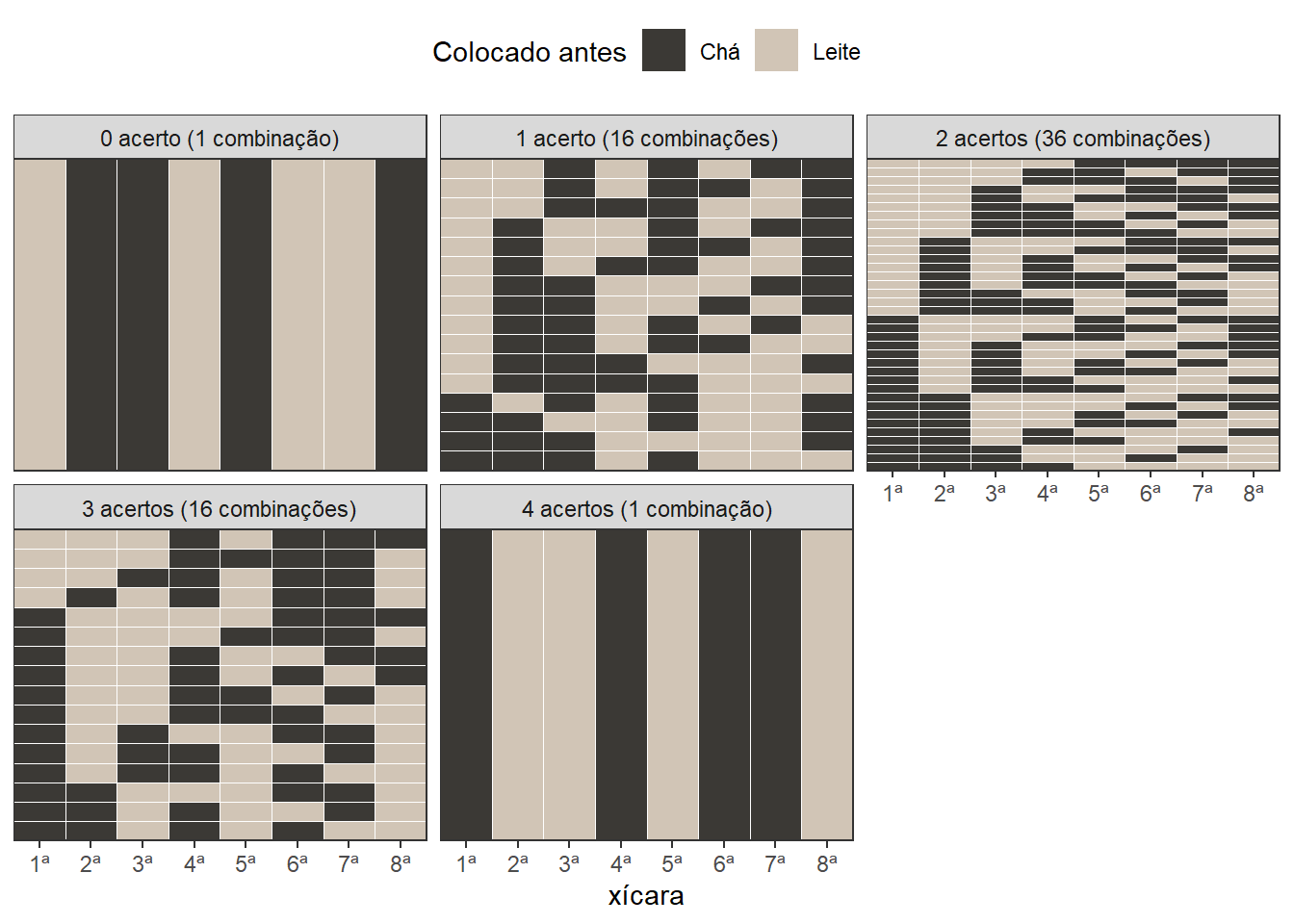
Sob a hipótese de que ela está escolhendo ao acaso, cada uma das 70 combinações possíveis teria a mesma probabilidade. Isso nos permite calcular a distribuição de probabilidades do número de acertos (
| x (n de acertos) | P(X = x) |
|---|---|
| 0 | 1/70 = 0.0143 |
| 1 | 16/70 = 0.2286 |
| 2 | 36/70 = 0.5143 |
| 3 | 16/70 = 0.2286 |
| 4 | 1/70 = 0.0143 |
Como a Dra. Bristol acertou as 4 xícaras, a probabilidade desse resultado ocorrer puramente por acaso é de apenas 1/70, ou 1.43%.
Em estatística, essa probabilidade de observar um resultado igual ou mais extremo que o obtido, assumindo que a hipótese nula é verdadeira, é chamada de p-valor.
Com um p-valor de 1,43%, o resultado observado apresenta uma forte discrepância em relação à hipótese do acaso. Em outras palavras, ou presenciamos um evento muito raro, ou a suposição de que ela estava apenas chutando não é a melhor explicação.
Se adotarmos como critério que resultados com probabilidade menor que 10% indicam habilidade, um acerto de 3 xícaras não seria suficientemente raro para rejeitar o acaso — afinal, a probabilidade de acertar ao menos 3 por sorte/ao acaso é de cerca de 24%, algo relativamente comum.
Conclusão
O experimento “Lady Tasting Tea” é mais do que uma curiosidade histórica — ele resume a lógica do teste de hipóteses:
Declare a hipótese do acaso (a hipótese nula).
Desenhe um experimento que permita calcular as probabilidades dos resultados sob essa hipótese.
Compare o resultado observado com o que era esperado.
Ver justamente a única combinação, dentre 70, que representa o acerto perfeito é um evento raro o bastante para colocar o acaso em dúvida. Isso não “prova” de forma absoluta que a habilidade da Dra. Bristol existe, mas oferece evidência estatística forte contra a explicação da sorte.
O mérito de Fisher foi criar um protocolo simples, randomizado e com regras claras, que transforma uma afirmação em uma questão testável de forma sistemática e reprodutível.